La Teoria dei Sistemi è nata intorno agli anni '40, a seguito di lavori multidisciplinari di diversi gruppi di scienziati. Il più famoso di questi gruppi, guidato dal matematico Wiener al MIT di Boston, comprendeva anche neuropsicologi, economisti e biologi, che indagavano sugli aspetti comuni delle loro scienze.
Wiener chiamò la nuova scienza "cibernetica". Il nome, di derivazione dal termine greco che significa "pilota della nave", era già stato usato da Ampere per indicare la "scienza del governo".
Da allora per "cibernetica" si è inteso lo studio del "controllo" nelle macchine e negli organismi viventi, mentre per Teoria dei Sistemi si intende una generalizzazione a tutti i campi dei concetti sviluppati in cibernetica. Al giorno d'oggi la Teoria Dei Sistemi copre un campo d'azione molto vasto, che sostanzialmente può toccare tutte le discipline. Per questo la sua definizione è estremamente generica, oppure in qualche modo imprecisa.
Una definizione interessante propone:
"La Teoria dei Sistemi è lo studio interdisciplinare dell'organizzazione astratta dei fenomeni, indipendentemente dalla loro sostanza e tipo [..]. Studia sia i principi comuni a tutte le entità complesse, sia i modelli che possono essere usati per descriverle"
da: "Principia Cybernetica Web" (adattata dall'Autore), http://pespmc1.vub.ac.be/DEFAULT.html
Sulle basi teoriche della Teoria dei Sistemi è costruita la "Teoria dei Controlli", che si occupa della realizzazione ottimale di sistemi di controllo, cioè di regolazione automatica.
Le applicazioni della Teoria dei Sistemi spaziano in molti campi e comprendono, oltre naturalmente alla regolazione automatica, molti campi dell'ingegneria, dell'economia, della gestione aziendale, delle scienze politiche, della psichiatria, della biologia e della ecologia.
Le nuove discipline che devono alcuni dei loro fondamenti alla Teoria dei Sistemi sono: la Robotica, l'Intelligenza Artificiale, le "Scienze della Complessità" e per qualche aspetto anche l'Informatica.
Sistemi e modelli Una definizione, molto generale, di "Sistema"Non ci sono definizioni di Sistema completamente soddisfacenti, ma il concetto è fecondo, a patto che non si inflazioni troppo il termine e non lo si usi mostrando di voler intendere tutto e non dicendo di fatto nulla.
Una definizione di Sistema è: "Ogni insieme definibile di componenti" (Maturana e Varela, 1979).
Questa definizione ci dice sostanzialmente che tutto è un sistema, ma pone con chiarezza la prima questione: un sistema è un insieme di "elementi", o "componenti" dei quali si potrà studiare l'organizzazione, il funzionamento e l'interazione (*).
Si può studiare cioè come, operando insieme, i componenti contribuiscono a determinare le caratteristiche del sistema complessivo. Ciascuno degli elementi che costituiscono un sistema può essere a sua volta un sistema ("sottosistema").
(*)
interazione = la modalità con cui due "entità" (sistemi!) si influenzano una con l'altra (inter-agiscono).Altre definizioni interessanti, abbastanza simili, sono le seguenti:
"Un Sistema è un insieme [..] di entità collegate o messe in relazione in modo tale da formare un'unità organica" (Iberall).
"Un Sistema è un insieme di elementi interagenti che assieme formano un tutt'uno (an "integrated whole")" (Hall e Fagen, 1956).
Queste definizioni rinforzano il fatto che i vari elementi del Sistema sono tenuti insieme da delle "relazioni", che determinano il comportamento globale del sistema e che, come vedremo, spesso assumono la forma di equazioni.
Un'altra cosa che spicca è che un sistema non deve essere necessariamente materiale, come un ponte o una pentola.
Esso può essere anche del tutto immateriale, come una frase o un'equazione algebrica.
Quando sarà necessario chiameremo "sistemi fisici" quelli che hanno almeno un elemento materiale e "sistemi astratti" i sistemi composti solo di elementi immateriali. Un'altra distinzione semplice, che possiamo fare fin da ora, è fra sistemi artificiali e naturali, intendendo per artificiali i sistemi prodotti con intenzione per uno scopo specifico, e per naturali gli altri.
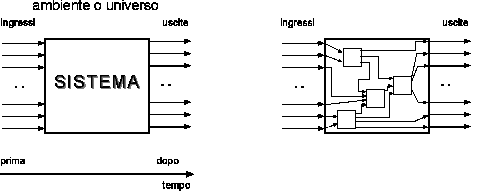
Il sistema come scatola neraVisto che la teoria parte da una definizione così generale di Sistema, si potrà dare un modo altrettanto generale di rappresentarlo graficamente. Ciò consiste nel disegnare un rettangolo, che rappresenta i "confini" esterni del sistema, entro al quale finiscono alcune frecce (ingressi) e dal quale escono altre frecce (uscite).
Disegnando questa "scatola" ("black box") non ne specifichiamo il contenuto, ma individuiamo soltanto gli elementi attraverso i quali il sistema interagisce con il resto dell'universo, cioè con quello che molti chiamano "l'ambiente" del sistema.
La descrizione di come funziona internamente il sistema potrebbe anche non interessarci. Di solito però è vero il contrario e siamo interessati ad "aprire la scatola", per capire come funziona il sistema e prevedere come si comporterà se sottoposto a determinati ingressi.
Una volta che siamo in grado di sapere come il sistema risponderà all'applicazione di certi ingressi saremo in grado di applicargli gli ingressi giusti per far sì che vada dove vogliamo. Saremo cioè in grado di "regolare" o "controllare" il sistema, perché dia i risultati voluti.

Figura 1: un sistema come "scatola nera" o "scatola grigia"
Analisi e SintesiDue termini che un tecnico dovrebbe saper usare con precisione, molto abusati nel linguaggio comune, forse anche più del termine "sistema" sono "Analisi" e "Sintesi".
Quando si parla di "analisi" si deve intendere lo studio dell'organizzazione e del funzionamento di un sistema.
I risultati di un'analisi sono: l'individuazione dei componenti fondamentali del sistema, la comprensione del funzionamento di quei componenti e del sistema generale che ne risulta e, molto spesso, un metodo per ottenere, in modo più o meno accurato, previsioni sul comportamento futuro del sistema.
Le attività dell'uomo sono sempre volte ad uno scopo, dunque l'analisi di un sistema non può essere l'unico scopo del suo studio. Dopo aver studiato un sistema ed aver capito come funziona la fase seguente è la sua "modifica" o "gestione" ai fini di raggiungere un certo obiettivo.
Questa fase viene spesso detta "sintesi".
Una buona definizione di "sintesi" è: "la formazione di un nuovo "intero", combinando parti separate":
Synthesis: The forming of a new and coherent whole by combining separate parts; and the ability to do so.
da "ArtLex Lexicon of Visual Art Terminology", in http://www.artlex.com/
Dunque la sintesi è il processo inverso dell'analisi. Se l'analisi fa a pezzi un sistema la sintesi lo mette assieme.
Nella successiva tabella si illustrano alcune occasioni nelle quali le parole analisi e sintesi sono usate con il significato che abbiamo loro attribuito in questo paragrafo.
|
Analisi (capire) |
Sintesi (fare) |
||
|
A. di un circuito |
Comprensione del funzionamento di un circuito elettronico |
S. di un circuito |
Realizzazione di un circuito elettronico che svolga le funzioni desiderate |
|
A. chimica |
Individuazione dei componenti di un materiale |
S. delle molecole |
Realizzazione di molecole progettate specificamente ed ottenute artificialmente |
|
A. politica |
studio delle cause dei fenomeni sociali |
Sintesi politica |
Formulazione di una legge, di un progetto o di "programma" politico |
|
A. psicologica |
studio della psiche di un essere umano |
S. psicologica |
La somma dei vari aspetti di una personalità |
|
A. grammaticale |
studio dell'organizzazione delle frasi e delle loro parole |
Scrittura |
La scrittura è la "sintesi" di frasi grammaticalmente e sintatticamente corrette |
Tabella 1: Analisi e sintesi
Ogni progetto richiede la valutazione di come ci si può aspettare che si comporti il sistema, cioè la sua analisi. Conoscendone i componenti, come funzionano assieme, e come vengono modificati dal progetto si può fare questa valutazione.
Lo scopo della fase di analisi dovrebbe perciò sempre essere quello di pervenire alla sintesi di sistemi artificiali aventi uno scopo preciso e ben progettati per quello scopo.
In sintesi ;-) : quando usato in ambito tecnico-scientifico il termine "Analisi" è legato al "capire", mentre "Sintesi" è sinonimo di "fare".
Il termine "sintesi" è usato spesso con significati diversi da quello che gli abbiamo attribuito.
Infatti nel vocabolario si trova "Sintesi: la proprietà di saper riassumere concetti complicati in frasi brevi" (da "Devoto-Oli, vocabolario della lingua italiana, Le Monnier) .
Per quanto questo significato sia riconducibile al nostro, rimane comunque abbastanza diverso. Questo ci illustra come le lingue naturali degli umani possano facilmente dar luogo ad ambiguità.
Un modello è un sistema che serve a risolvere un problema su un altro sistema. Vediamo come ciò è possibile, illustrandone una definizione precisa:
Dati un sistema ed un problema da risolvere su di esso un modello del sistema è un altro sistema, più semplice, che si comporta in modo simile al sistema originario, con l'accuratezza sufficiente per risolvere il problema.
Il modello è quindi un modo di descrivere il sistema che ne trascura tutte quelle caratteristiche che non hanno importanza per lo scopo per cui lo creiamo.
A differenza di un Sistema "generale", che potrebbe esistere anche se non serve a nulla, un modello ha una definizione essenzialmente operativa, serve a "farci qualcosa", altrimenti non verrebbe neppure inventato.
Dato che riproduce il comportamento del sistema originario, si può usare il modello invece del sistema per "provarne" il funzionamento. Ciò può aiutare molto nella realizzazione del fine che si prefigge.
Un modello può essere molto diverso nell'aspetto al sistema originario, può essere fatto con materiali e tecniche del tutto diverse. Addirittura un modello di un sistema fisico può essere astratto; l'importante è che ne riproduca in un modo sufficientemente accurato il comportamento.
Tanto più i modelli sono accurati, nel senso che riproducono con migliore approssimazione il comportamento del sistema da studiare, tanto più sono "costosi". Ciò significa che fare modelli più accurati del necessario significa quasi sempre "spendere" di più.
C'è da notare anche che ad uno stesso Sistema si possono associare diversi modelli, che possono servire a risolvere problemi diversi o a risolvere lo stesso problema con diversa accuratezza. Inoltre un modello può aiutare a risolvere più di un problema.
Vediamo un esempio piuttosto dettagliato, che analizza diversi tipi di modello per lo stesso sistema:
|
Sistema |
Problema |
Modello |
|
Modellino in scala per studi aerodinamici in galleria del vento |
||
|
Deve consumare poco |
Modello matematico per studi aerodinamici al computer |
|
|
Prototipo del motore per sperimentazioni pratiche |
||
|
Prototipo dell'intera autovettura per collaudi "sul campo" |
||
|
Automobile |
Deve essere comoda |
Prototipo dei sedili e manichino interno della vettura |
|
Prototipo dell'intera autovettura per collaudi "sul campo" |
||
|
Schizzi "artistici" dell'aspetto della vettura |
||
|
Deve essere attraente |
Disegno CAD 3D |
|
|
Prototipo delle singole parti |
||
|
Prototipo dell'intera carrozzeria |
Tabella 2: Modelli diversi per lo stesso sistema (e per lo stesso problema!)
Per concludere il paragrafo riportiamo una definizione di modello molto elegante, anche se un po' involuta:
If a System describes, simulates or predicts a portion of his environments it may be regarded as a MODEL of that portion.
da: "Principia Cybernetica Web"
Ogni sistema è in qualche modo "immerso" in un ambiente esterno con il quale interagisce attraverso i suoi ingressi e le sue uscite. Esso ha perciò un "limite" che individua il confine che lo separa dal mondo esterno.
Nella rappresentazione a scatola nera (Figura 1) il limite è il rettangolo.
Come esempi di limite fra sistema e ambiente possiamo considerare: l'invaso di un bacino idroelettrico, la membrana di una cellula, il confine di uno stato, i muri di una stanza.
Esempi di "elementi", o "componenti", di cui sono costituiti i sistemi possono essere: gli ingranaggi di un cambio, le "parti sociali" in una società, elettroni, neutroni e protoni in un atomo.
I componenti possono classificati come ingressi, uscite ed elementi di "accumulazione",.
Gli ingressi sono elementi che apportano al sistema energia, materia o informazione, mentre le uscite le tolgono al sistema applicandole all'ambiente.
Gli elementi di accumulazione ("reservoirs", serbatoi), possono immagazzinare energia, materia o informazione, per esempio l'acqua in un bacino idroelettrico (materia e energia potenziale), il grano in un silos (materia), la memoria in un computer (informazione), il DNA di una cellula (informazione), la temperatura in una stanza (energia interna), il denaro in una banca ("energia" (in senso lato!)), i grassi del corpo (energia).
Ogni sistema ha una "rete di comunicazione", che permette lo scambio di energia, materia o informazione con il mondo esterno e fra i componenti interni. Come esempi di reti di comunicazione si possono considerare: le condotte forzate di un impianto idroelettrico, le tubazioni del silos, i fili elettrici su una scheda di un computer, l'RNA messaggero, i tubi di un impianto di riscaldamento, la cassa in una Banca, le vene.
Cause ed effetti: ingressi ed usciteDalla nostra descrizione schematica di un sistema è chiaro che le cause di ciò che avviene al sistema sono gli ingressi, unica via attraverso cui entra qualcosa dall'esterno, e gli effetti sono le uscite.
Gli ingressi (input) sono il risultato dell'influenza dell'ambiente sul sistema, le azioni che l'ambiente esterno esercita sul sistema.
Le uscite (output) sono il risultato dell'influenza del sistema sull'ambiente, cioè le misure disponibili all'esterno.
Naturalmente le cause devono precedere temporalmente gli effetti e perciò una variazione delle uscite deve avvenire dopo la variazione nell'ingresso che la causa. Ciò spiega l'asse dei tempi riportato nella Figura 1, nella quale gli ingressi, a sinistra, precedono, anche nel tempo, le uscite, a destra.
Il ritardo con cui gli ingressi influenzano le uscite è una delle caratteristiche tipiche dei sistemi e ci fa immaginare che gli "elementi" del sistema non possano essere solo ingressi e uscite, ma che ci debba essere anche qualcos'altro all'interno che causa questo ritardo. Infatti abbiamo già visto che si possono individuare anche elementi di "accumulazione", sui quali torneremo ancora in seguito.
In alcuni casi ideali l'uscita può variare contemporaneamente all'ingresso, questo non può accadere per un sistema fisico, dato che lo impediscono i principi della termodinamica.
Spesso però si può fare l'approssimazione di considerare che le uscite vengano generate contemporaneamente agli ingressi che le causano, cioè che un sistema non abbia "ritardi".
Senz'altro non si potrà ipotizzare, nemmeno per approssimazione, che le uscite precedano nel tempo gli ingressi che le causano, dato che l'esperienza ed i principi della fisica dimostrano che i sistemi fisici sono "causali" o "non anticipativi".
Può capitare che la distinzione fra ingressi e uscite non sia obbligata: una grandezza potrebbe essere considerata sia ingresso che uscita.
In questi casi si segue un criterio utilitaristico: si distingue fra ingresso e uscita come fa più comodo. Naturalmente devono essere rispettati i vincoli di causalità: le grandezze che sono scelte come ingressi devono effettivamente influenzare quelle scelte come uscite del sistema. Si veda in proposito l'esempio della legge di Ohm, nel successivo paragrafo "Variabili e parametri"
E' possibile che le uscite non "dicano tutto" del comportamento del sistema, cioè che alcuni effetti dell'evoluzione di un sistema possano non essere "visibili" all'esterno. In questi casi non è possibile vedere l'evoluzione di elementi interni del sistema osservandone solo le uscite.
Per esempio: può essere difficile, o anche impossibile per un medico stabilire la diagnosi di una malattia basandosi solo sui sintomi che essa causa.
Le uscite sono perciò il risultato dell'evoluzione delle sole parti "osservabili" del sistema.
Per esempio il risultato di un calcolo matematico, come la semplificazione di un'espressione algebrica, si può considerare l'uscita del sistema "semplificazione di un'espressione". In questo sistema l'ingresso è l'espressione non semplificata, l'uscita è quella semplificata. Se consideriamo il sistema in questo modo l'uscita non può dire nulla sull'evoluzione della soluzione, cioè sui passaggi che si sono fatti per giungervi.
Risposta di un sistema
L'evoluzione nel corso del tempo degli ingressi applicati ad un sistema viene detto "eccitazione" o "sollecitazione" del sistema.
L'evoluzione delle uscite nel corso del tempo in conseguenza di una ben determinata eccitazione, viene detta risposta del sistema a quella eccitazione.
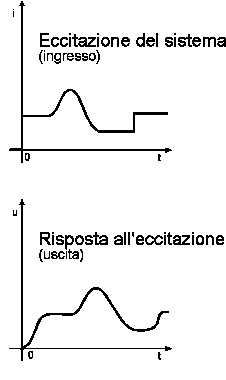 Figura 2: eccitazione e risposta
Figura 2: eccitazione e risposta
Un sistema che non ha alcuna comunicazione con l'esterno, che non scambia con l'ambiente né energia, né materia, né informazione, viene detto "sistema chiuso". Un sistema chiuso è dunque del tutto tagliato fuori dal suo ambiente, non ha né ingressi né uscite.
Di converso "aperto" è un sistema che è in relazione con il resto dell'universo. Viene modificato dal suo ambiente e lo modifica.
Se un sistema non ha uscite ciò non significa che è chiuso ma solo che non è osservabile dall'esterno.
Non esistono in natura, per ragioni fisiche fondamentali, sistemi in grado di rimanere perfettamente isolati dal loro ambiente. Per questo gli unici sistemi chiusi "perfetti" sono sistemi astratti, che possono essere usati come modelli approssimati di sistemi fisici reali. Per moltissime applicazioni questi modelli chiusi possono essere sufficientemente accurati.
Come esempio di questa ultima affermazione prendiamo i due sistemi termici illustrati nella Figura 3. Il sistema (a) è un forno elettrico per la cottura degli alimenti, mentre (b) è un calorimetro.
Il forno deve essere considerato un sistema aperto in quanto:
- durante il periodo in cui interessa studiarlo deve entrare energia termica attraverso il resistore scaldante
- l'isolamento non potrà essere molto efficace, dato che il forno dovrà avere un costo accettabile
- il forno dovrà funzionare per tempi relativamente lunghi.
Il modello con cui si analizzerà il forno dovrà essere un sistema aperto.
Il calorimetro (b) è invece un sistema nel quale viene bruciato un alimento al fine di misurare l'energia che contiene. Esso si può considerare un sistema chiuso, con buona approssimazione, in quanto:
- l'energia in gioco proviene in gran parte dalla combustione dell'alimento all'interno del calorimetro, se si trascura una piccola quantità di energia usata per "accenderlo"
- l'isolamento termico è buono, anche se non perfetto, perché il calorimetro è fatto per disperdere il meno possibile
- l'energia sprigionata dalla combustione è comunque molto maggiore di quella perduta per dispersione
- l'esperimento ha una durata relativamente breve.
Utilizzare un modello chiuso, come quello indicato in Figura, per studiare il calorimetro potrà perciò dare errori accettabili.
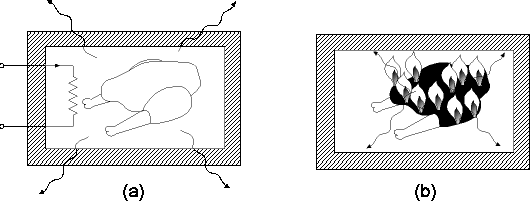
Figura 3: sistema termico aperto (a) o chiuso (b)
Un sistema chiuso può evolvere solo a spese della sua energia interna; dato che non ha ingressi non può acquisirne dall'esterno. Se raggiunge l'equilibrio (vedi oltre) lo mantiene per sempre.
Variabili e parametri
La Teoria dei Sistemi è una scienza esatta e come tutte le scienze esatte fa uso di grandezze numeriche, che possono essere misurate sul sistema. Queste grandezze rappresentano in ogni istante la quantità di energia, materia o informazione che si può assegnare a ciascuno degli elementi del sistema.
Una variabile è una grandezza del sistema il cui valore può cambiare in ogni istante di tempo. In ogni istante si può assegnare un valore numerico ad una variabile effettuandone una misurazione, almeno idealmente (possono esistere vincoli fisici che ne rendono impossibile la misurazione pratica).
Gli ingressi e le uscite di un sistema sono variabili di quel sistema.
Si fa notare il "può" nella definizione di variabile. Ciò significa che le variabili possono anche assumere valori che non cambiano nel corso di intervalli di tempo più o meno lunghi.
Come esempio consideriamo un'automobile durante un lungo viaggio autostradale. Anche se il guidatore mantiene una velocità di 130 km/h, fissa per 6 ore la velocità è pur sempre una variabile del sistema, che "occasionalmente" è rimasta fissa.
Un parametro è una grandezza che ci permette di distinguere fra due sistemi che sono organizzati nello stesso modo ma si comportano in modo diverso.
Perciò due sistemi che funzionano nello stesso modo differiscono solo per l'effetto del valore diverso dei loro parametri.
I parametri sono quei valori che distinguono due sistemi diversi che hanno la stessa struttura.
Per chiarire prendiamo per esempio una molla "morbida" ed una "dura". Entrambi i sistemi sono molle, cioè oggetti che generano una forza proporzionale a quanto sono compressi. Funzionano perciò entrambi in modo identico (sono organizzati nello stesso modo) ma si comportano in modo diverso solo per il fatto che hanno rigidità diversa.
Il valore numerico che si può assegnare alla caratteristica che distingue fra i due sistemi, cioè la costante di elasticità delle due molle, è perciò un parametro del sistema "molla".
Si può dire che le due molle hanno modelli uguali. I due modelli hanno però un parametro diverso.
Il modello di una molla si può esprimere in termini matematici in questo modo:
F = - k x
dove F è la forza che la molla applica sugli altri sistemi che le si collegano, k è la costante di elasticità della molla, x è lo spostamento dell'estremo della molla rispetto alla sua posizione di riposo.
Se due molle hanno il parametro k diverso sono una più "dura" dell'altra, dato che a parità di spostamento una risponde con una forza maggiore dell'altra.
Nella trattazione matematica dei sistemi si considera che i parametri siano valori fissi, che non cambiano mai nel corso di tutto il periodo di tempo nel quale si è interessati al sistema. In questo caso vengono detti "costanti".
La definizione di parametro che abbiamo dato si applica anche in altri casi. Per esempio si chiamano "parametri" i valori che si passano alle procedure informatiche (si pensi alla sintassi dell'istruzione "procedure" in Pascal). Ogni volta che si usa una procedura si possono cambiare i suoi parametri. Passare parametri diversi Dunque, dato che cambiare i parametri modifica il comportamento della procedura, l'uso della parola "parametro" nelle procedure informatiche rispetta perfettamente la definizione precedente.
Per tutti i fini pratici si possono considerare parametri di un sistema tutte quelle quantità che sono "fisse" nel periodo di tempo nel quale interessa studiare il sistema.
Il termine "fisse" fra virgolette sta a significare che sono grandezze effettivamente costanti oppure che variano in modo tanto lento da poterle considerare costanti nel modello che utilizziamo.
Tipici esempi di parametri di un sistema possono essere le caratteristiche dei materiali, quali l'elasticità la resistenza a rottura, la costante di dilatazione termica. Questi parametri si considerano sempre costanti per ogni materiale, sono diversi solo se si cambia materiale.
Se si volesse obiettare si potrebbe dire che le grandezze che abbiamo appena elencato non sono davvero costanti, perché i materiali "invecchiano". Questa obiezione è risolta in due modi:
- considerando tempi talmente brevi da poter trascurare l'invecchiamento
- considerando che il comportamento del sistema varia nel corso del tempo, quando variano i parametri (*).
(*)
Questa opzione equivale a considerare il sistema "variante nel tempo", come vedremo in seguito.Le variabili di un sistema sono distinguibili in due tipi: variabili di flusso e variabili di livello.
Le variabili di flusso rappresentano quegli elementi del sistema che sono in grado di trasferire energia, materia o informazione all'interno ed all'esterno del sistema. Tipicamente hanno l'unità di misura del flusso, cioè della grandezza per unità di tempo; per esempio la portata d'acqua in una conduttura, il calore che entra in una stanza, il numero di bit al secondo trasferito fra due computer, il denaro che entra in una Banca in un giorno, le calorie di alimenti che mangiamo durante un pasto.
Le variabili di flusso fanno cambiare nel corso del tempo il valore delle variabili di livello. Per esempio le portate in ingresso ed in uscita alzano o abbassano il livello di un serbatoio d'acqua, il calore cambia la temperatura di una stanza, la memoria di un computer si riempie di numeri, la cassa di una Banca accumula denaro, il corpo accumula grasso. Il livello dell'acqua, la temperatura, la memoria, il capitale o il grasso accumulato sono le variabili di livello degli esempi precedentemente elencati.
Quindi le variabili di livello sono in grado di accumulare energia, materia o informazione e assumono in qualche modo il significato di "memoria" del sistema.
|
Variabile di flusso |
Variabile di livello |
|
Portata di un fluido |
Livello del fluido |
|
Corrente elettrica in un condensatore |
Tensione elettrica sul condensatore |
|
Flusso magnetico in un induttore |
Corrente elettrica nell'induttore |
|
Calore |
Temperatura |
|
Profitti o perdite |
Capitale |
|
Cibo ingerito |
Grasso |
|
Spostamento di un oggetto (velocità) |
Altezza dell'oggetto |
Tabella 3: variabili di flusso e di livello
In matematica e nel parlare tecnico è frequente l'uso dei termini "variabile dipendente" e "variabile indipendente".
Le variabili indipendenti, o incognite, sono quelle su cui si ha libertà d'intervento, i valori che si possono decidere a piacimento. Dato che si ha la libertà di fissare ogni valore per le incognite, esse sono "variabili" nel senso definito precedentemente.
Riguardando la definizione di "ingresso" (in 1.2.1), ci si rende conto che il termine "variabile indipendente" è un altro modo per esprimere, nel campo della matematica, il concetto di "ingresso".
In matematica si denotano i risultati delle equazioni come "variabili indipendenti". I valori delle variabili indipendenti sono determinati una volta decisi i valori delle incognite.
Dunque la causa del valore delle variabili indipendenti è il valore delle incognite e possiamo far coincidere il concetto di variabile indipendente con quello di "uscita" del sistema.
Nelle situazioni reali è spesso difficile distinguere fra variabili e parametri, dato che sono tutte grandezze fisiche apparentemente analoghe.
Inoltre le cose si complicano quando, come avremo modo di vedere più avanti in alcuni tipi di sistemi, il tempo non entra in gioco, per cui le variabili non variano :-( .
Come capire quali sono le variabili e quali i parametri?
Torniamo alle definizioni: le variabili "possono" variare, mentre i parametri possono assumere un solo e ben determinato valore. Le variabili sono suscettibili assumere di qualsiasi valore, anche se incidentalmente nel corso dell'evoluzione di un sistema ne assumono solo uno.
Prendiamo per esempio un'equazione di primo grado:
a x = b
Se consideriamo che a e b assumano valori fissi e x possa variare a e b sono parametri, x è una variabile.
Naturalmente perché sia vera l'uguaglianza x deve sempre valere b/a; anche x è perciò un valore unico, ma non "fisso" nel senso definito precedentemente.
I matematici, che danno alle equazioni un significato del tutto astratto, di solito assegnano alle variabili nelle equazioni il "nome" x, ma ciò non è per nulla obbligatorio.
I tecnici, che usano le equazioni per scopi pratici, assegnano alle variabili ed ai parametri simboli più significativi.
La legge di Ohm, per esempio, è un'equazione di primo grado, analoga alla precedente:
R i = V
in questa equazione il ruolo della variabile può essere giocato da uno qualsiasi dei simboli coinvolti, in dipendenza del problema che si deve risolvere.
Illustriamo tre problemi nei quali ingresso, parametro e uscita sono grandezze diverse, anche se il modello del sistema è sempre la legge di Ohm.
|
Problema |
Ingresso |
Uscita |
Parametro |
|
|
1 |
Misurare una corrente |
Tensione |
Corrente |
Resistenza |
|
2 |
Limitare una corrente |
Corrente |
Resistenza |
Tensione |
|
3 |
Dimensionare un carico alimentato da una cella fotoelettrica |
Resistenza |
Tensione |
Corrente |
Tabella 4: variabili, ingressi e parametri in diverse applicazioni della legge di Ohm
1) Dato che al giorno d'oggi è molto facile misurare accuratamente la tensione, di solito la misura della corrente elettrica viene effettuata leggendo la tensione prodotta dalla corrente da misurare su un resistore campione, la cui resistenza è nota. Perciò se il problema è la misura della corrente il valore della resistenza (noto e fisso) è il parametro del sistema, il valore di tensione misurato è la variabile indipendente (ingresso) ed il valore calcolato con la legge di Ohm è la variabile dipendente (uscita). Dunque l'uscita può essere determinata con l'equazione i = V / R.
2) Durante il progetto elettrico ed elettronico spesso si deve dimensionare un circuito in modo che in un suo certo ramo non scorra mai una corrente superiore ad un certo valore. Spesso in questi casi la tensione è stabilita a priori (si pensi alla tensione della rete elettrica, che è sempre di 220 Volt (*)). Dunque la tensione sarà il parametro del sistema, la corrente massima da erogare la variabile indipendente. La resistenza da mettere nel circuito, che consideriamo l'uscita del sistema "dimensionamento del circuito" sarà determinata risolvendo l'equazione secondo R, cioè: R = V / i.
(*) di valore efficace!
3) Esistono dispositivi, come le celle fotoelettriche per la produzione di energia elettrica, che erogano una corrente costante e fanno variare la tensione elettrica ai loro capi in base all'energia che sono in grado di sviluppare al momento.
Se conosciamo la corrente erogata dalla cella fotoelettrica e la resistenza del "carico" del circuito possiamo determinare la tensione e quindi, per altre vie che qui non vogliamo indagare, la potenza elettrica erogata e stabilire se essa è sufficiente per la nostra applicazione.
Dunque in questo caso la corrente è il parametro del sistema, la resistenza del carico l'ingresso, la tensione l'uscita, che sarà determinata con l'equazione V = R i.
Equilibrio e sistemi all'equilibrioUn sistema è in condizione di equilibrio quando "non cambia". Il senso di questo "non cambiare" si precisa meglio distinguendo fra equilibrio statico ed equilibrio dinamico.
Un sistema è in una condizione di equilibrio statico quando tutte le "forze" applicate su di esso sono bilanciate.
Le "forze" di cui si parla nella definizione sono gli ingressi applicati al sistema.
Dunque se gli ingressi sono costanti e tutte le altre variabili del sistema si mantengono costanti il sistema è in equilibrio statico.
Per esempio, una popolazione nella quale non avvengono né nascite né morti è in equilibrio statico, così come un pendolo fermo nella sua posizione più bassa.
In un equilibrio statico il sistema è completamente fermo, non succede nulla. Gli ingressi, le uscite ed anche le variabili interne del sistema non variano.
Un sistema sempre in equilibrio statico viene detto sistema statico.
Un sistema statico non può "muoversi", nel senso più generale del termine. In un sistema statico si considera che gli ingressi siano applicati da sempre e per sempre e che le uscite conseguenti siano sempre quelle.
Per esempio: una costruzione edile è un sistema statico, dato che rimane ferma "per sempre" (almeno così si spera!). Peraltro il sistema non può essere considerato statico se contempliamo che la costruzione sia sottoposta ad un terremoto :-( .
Un sistema che può non essere in equilibrio statico viene detto sistema dinamico.
Dunque un sistema dinamico ha la possibilità di "muoversi", anche se non è escluso che per tempi più o meno lunghi si trovi in condizioni di equilibrio statico.
In un sistema dinamico possono esistere molti punti di equilibrio. Nel suo "movimento" un sistema dinamico si può spostare nelle vicinanze dei suoi punti di equilibrio; se i suoi ingressi si mantengono costanti ogni sistema fisico finisce, nel lungo periodo, in un punto di equilibrio.
La radice etimologica della parola "dinamico" è nel greco "dynamikos", il cui significato è derivato da "forza" ("dynamis"). Nel gergo tecnico - scientifico, ed ora anche nel linguaggio comune, la parola dinamico è sempre associata al movimento e viene contrapposta per contrasto alla parola statico, che proviene anch'essa dal greco, "statikos", che significa "atto a fermare".
I sistemi dinamici possono avere anche un altro tipo di equilibrio, detto equilibrio dinamico.
In un equilibrio dinamico gli ingressi cambiano ma sono controbilanciati dalle uscite ed il sistema è in condizioni di "crescita zero".
In condizioni di equilibrio dinamico viene mantenuto un "livello" mediamente costante, nel lungo periodo non si accumula energia, materia o informazione nel sistema.
Portiamo due esempi: una popolazione nella quale avvengono lo stesso numero, variabile, di nascite e di morti è in equilibrio dinamico.
In una famiglia "in equilibrio" il tenore di vita deve essere tale che le spese siano pareggiate dai redditi. Il sistema ha ingressi variabili nel tempo (gli stipendi e gli altri introiti), ed anche spese (uscite) non sono costanti ma nel lungo periodo lo stile di vita della famiglia è tale da far sì che le uscite siano adeguate agli ingressi.
Un sistema in equilibrio dinamico viene detto in condizioni stazionarie (steady state o stationary state).
Stabilità degli equilibri
I punti di equilibrio di un sistema si possono distinguere in stabili ed instabili.
Immaginiamo di porre un sistema in una condizione di equilibrio. Supponiamo in seguito di disturbare l'equilibrio del sistema con una piccola variazione di un ingresso, cioè di applicare al sistema un ingresso diverso da quello cui corrisponde l'equilibrio.
Se sistema così "sbilanciato" si mantiene vicino all'equilibrio iniziale allora l'equilibrio è stabile. Se, al contrario, il sistema si allontana dall'equilibrio esso è instabile.
Un punto di equilibrio è instabile se il sistema tende ad allontanarvisi indefinitamente quando viene perturbato.
Un punto di equilibrio è stabile se il sistema, sia pur perturbato, continua a rimanere in un suo intorno.
Per cui se un sistema è in un equilibrio stabile e viene disturbato, una volta rimosso il disturbo esso torna al punto di equilibrio o tutt'al più continua a muoversi in un suo intorno.
Si può anche definire un equilibrio neutro, o indifferente, nel quale dopo la rimozione del disturbo il sistema rimane nel punto in cui si era portato quando il disturbo era presente.
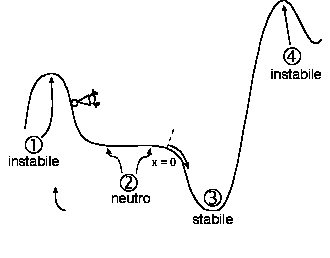
Figura 4: un punto si muove su una traiettoria
Consideriamo come esempio il carrello per montagne russe illustrato in Figura 4. Il carrello è vincolato ad un binario e perciò si può muovere solo in direzione tangenziale alla traiettoria.
Se immaginiamo di mettere il carrello nel punto 3, in fondo alla gola più bassa, e pensiamo di spingerlo un poco, ci rendiamo conto che il sistema reale deve tornare nel punto di equilibrio stabile, dato che la forza di gravità lo farà muovere verso il punto più basso e l'attrito lo farà fermare proprio in quel punto dopo un certo numero di oscillazioni.
Consideriamo ora il caso ideale, non riscontrabile in un sistema fisico, in cui l'attrito non esiste. Se la spinta che diamo al carrello è abbastanza piccola esso, in assenza di attrito, continuerà ad oscillare per l'eternità intorno al punto di equilibrio, che perciò è stabile, dato che il carrello si mantiene in un intorno del punto di equilibrio.
Spostiamo ora il carrello esattamente sulla sommità dei picchi, in uno qualsiasi dei punti 1 o 4. Se il carrello è fermo in uno di quei punti la sua forza peso è tutta scaricata sul binario, per cui il carrello rimane fermo. I punti 1 e 4 sono perciò punti di equilibrio statico.
Ma se immaginiamo di dare una spinta, anche piccola, al carrello esso si allontana dall'equilibrio senza più ritornarci. I punti 1 e 4 sono perciò punti di equilibrio instabile.
Infine immaginiamo di essere in condizioni di attrito e di mettere il carrello in uno qualsiasi dei punti del tratto piano indicato dal numero 2 nel disegno di Figura 4. In questo caso una piccola spinta farà fermare il sistema in un altro punto di equilibrio, lì vicino. Perciò se il sistema è sottoposto all'attrito l'equilibrio nella zona 2 è neutro.
Peraltro se si trascura l'attrito una forza anche piccola applicata al carrello lo farà muovere senza fermarsi, per cui finirà per cadere nella gola 3, allontanandosi dalla posizione iniziale. Perciò se trascuriamo l'attrito i punti della zona 2 sono punti di equilibrio instabile.
Questo esempio ci fa capire come in generale la stabilità di un equilibrio dipenda dall'entità del disturbo applicato. Se il disturbo è tale da superare una certa soglia può far partire il sistema verso un altro equilibrio vicino.
Infatti, se guardiamo ancora la Figura 4, ci rendiamo conto che dal punto 3, con una spinta sufficientemente forte, è possibile, per esempio, far superare al carrello il picco 4. In questo caso la posizione del sistema non rimane più confinata in un intorno di 3, per cui l'equilibrio, in presenza di un disturbo sufficientemente grande, diventa instabile.
StatoTutto ciò che abbiamo definito finora porta in modo abbastanza naturale alla definizione di uno dei concetti più fecondi della Teoria dei Sistemi: il concetto di "stato".
In letteratura si trovano molte definizioni di "stato", diverse fra loro.
Quella che ha la preferenza dell'Autore è data da Marro ed è la seguente:
"Lo stato è l'informazione di cui occorre disporre istante per istante per poter predire l'effetto della storia passata del sistema sull'andamento futuro delle uscite" (da Marro: "TEORIA DEI SISTEMI Fondamenti", Patron Bologna).
Il concetto di stato, nella forma indicata da questa definizione, è basato sul fatto che gli eventi del passato possono influenzare il futuro solo se lasciano fisicamente qualche traccia di sé all'interno del sistema.
Lo stato è quindi tutto quello che occorre e basta per tenere traccia del passato del sistema ai fini di prevederne il comportamento futuro.
Le variabili di stato di un sistema mostrano ciò che si è "accumulato" nel sistema nel corso del tempo, pertanto sono variabili "di livello", nel senso definito precedentemente.
Dato che lo stato di un sistema è la manifestazione di ciò che nel passato ha lasciato traccia sul sistema esso può essere considerato la sua "memoria".
Vediamo un esempio, che può aiutare a chiarire la definizione di stato. Esso riguarda gli affari in borsa del Sig. Rossi.
Il Sig. Rossi si diletta di speculazioni finanziarie. Un anno fa ha comprato 50 azioni della A.C.M.E. s.p.a., poi ne ha vendute 40 dopo 4 mesi e comprate 10 il mese scorso. Oggi deve decidere se vendere le sue 20 azioni o se tenersele.
La decisione è "semplice": se il Sig. Rossi pensa che in futuro le A.C.M.E. s.p.a. aumenteranno, allora le tiene, se pensa che caleranno le vende. Per prendere questa decisione il Sig. Rossi non deve considerare se aveva comprato le azioni ad un prezzo più alto o più basso di quello odierno. Infatti se Rossi pensa che caleranno e non le vende per il solo fatto che oggi non ci guadagna, è probabile che di rimetterà ancora più di quanto ci rimetterebbe oggi, se le azioni caleranno davvero.
L'unica cosa che interessa per il futuro delle speculazioni del Sig. Rossi è ciò che egli possiede oggi; non importa né se ha fatto un buon affare o meno nel passato, né se nel passato ha avuto 40, 50, 20 azioni o nessuna. Importa solo che oggi egli possiede 20 azioni della A.C.M.E. s.p.a. e quanto costa un'azione oggi.
Il prezzo dell'azione ed il numero delle azioni possedute sono quindi due elementi dello stato del sistema tramite il quale il Sig. Rossi prende la sua decisione.
La decisione sarà basata su un modello dell'andamento delle azioni A.C.M.E. s.p.a., che il Sig. Rossi ha, in testa o nel suo computer, e che è basato in qualche modo sull'"esperienza" passata. Questo modello può avere come ingressi per esempio: l'andamento nel tempo dell'azione, informazioni sull'azienda, quali per esempio i bilanci, informazioni generali sull'economia e la situazione politica del paese in cui lavora la A.C.M.E. s.p.a., che potrebbero influenzare l'andamento della borsa. Lo stato, come già visto, sarà costituito da prezzo e numero di azioni possedute, l'uscita sarà una variabile che può assumere, per ogni azione, solo due valori: "vendere" o "tenere".
Consideriamo ora di "fotografare" idealmente un sistema in un certo istante, "congelando" il valore di tutte le sue variabili. Se conosciamo il valore delle variabili di stato in questo istante abbiamo, data la definizione, tutto ciò che serve del passato per studiare il comportamento del sistema.
Se ora pensiamo di "far ripartire" il sistema dopo il congelamento non abbiamo bisogno di conoscere del passato altro che i valori delle variabili di stato nel momento della nuova partenza, che sono le stesse del momento del "congelamento", dato che il sistema è stato bloccato.
I valori delle variabili di stato di un sistema nell'istante dal quale si considera di ripartire sono perciò le condizioni iniziali del sistema. Se si considera che il sistema parta da quelle condizioni si hanno i dati sufficienti, conoscendo anche gli ingressi che applicheremo ed avendo un buon modello del sistema, a prevederne il comportamento.
Quando conosciamo le condizioni iniziali, allora davvero il passato è "passato".
Vediamo ora un altro esempio ed identifichiamo le variabili di stato di un sistema meccanico.
Consideriamo un oggetto in caduta libera. Se trascuriamo l'effetto dell'attrito l'oggetto cade con accelerazione costante, pari all'accelerazione di gravità. Di conseguenza il valore della velocità sarà proporzionale al tempo trascorso.
Come abbiamo appena spiegato le variabili di stato sono le condizioni iniziali che ci permettono di specificare completamente la condizione dalla quale si fa partire un esperimento sul sistema.
Per sapere in ogni istante dov'è un grave in caduta libera dobbiamo senz'altro sapere dov'è nell'istante iniziale. Quindi è necessario conoscere la posizione iniziale, che chiameremo x(t0), o anche x0 (x(t0) = x0).
La posizione iniziale non basta, perché l'oggetto potrebbe prima andare verso l'alto, poi cadere, in base alla velocità che ha nell'istante di inizio. Dobbiamo perciò sapere anche la velocità iniziale del grave, che chiameremo v(t0), o anche v0 (v(t0) = v0).
Dunque per determinare la posizione del grave in ogni istante ci servono: la posizione e la velocità dell'oggetto all'istante iniziale, il valore della forza di gravità, che considereremo l'ingresso, ed un buon modello del sistema. Non servirà, per esempio, l'accelerazione, perché essa si può ricavare dalle altre grandezze.
Allora, per quanto detto precedentemente, la posizione e la velocità iniziale sono i due elementi dello stato che stavamo cercando.
A questo si può trovare conferma ricordando l'espressione del moto di un grave, note dalla Fisica elementare. Un buon modello del sistema, in assenza di attrito, è infatti rappresentato dalle seguenti equazioni:
x (t) = x(t0) + v(t0) (t - t0) – ½ g (t - t0)2
v(t) = v(t0) – g (t - t0)
dove: t è il valore del tempo in un qualsiasi istante, che può essere un numero qualsiasi
t0 è il tempo dell'istante iniziale, che assume un solo valore ben determinato (spesso si assume che sia t0=0)
x (t) è valore della posizione in un qualsiasi istante t
v(t) è il valore della velocità in un qualsiasi istante t
x (t0) e v(t0) sono i valori della posizione e della velocità nell'istante istante t0, cioè le due condizioni iniziali
del sistema
g è il valore dell'accelerazione di gravità, che determina la forza peso, che può essere considerata l'ingresso del sistema
Lo stato del sistema è quindi l'insieme dei valori della sua posizione e della sua velocità in ogni istante, cioè l'insieme delle funzioni x(t) e v(t).
Riprendiamo ora l'esempio delle montagne russe (vedi Figura 4). Dato che il carrello è vincolato a mantenersi sulla traiettoria del binario, possiamo immaginare di "stendere sul binario" un asse delle x, rispetto al quale è riferita ogni posizione e velocità (l'origine della coordinata x è indicata dalla scritta x = 0 nella Figura 4 e la sua direzione dalla freccia che segue la traiettoria). Con considerazioni analoghe alle precedenti si può concludere che anche in questo caso lo stato del sistema è dato dalla posizione e dalla velocità lungo la traiettoria (*).
(*) La cosa è del tutto generale. Lo stato di ogni sistema meccanico comprende due valori per ogni "grado di libertà". Un grado di libertà è una "direzione" in cui il sistema si può muovere, una variabile che il sistema può far "muovere". P.es. un pendolo ha un solo grado di libertà, perché durante il suo movimento varia solo un angolo, così come il carrello di Figura 4, ove varia la coordinata sulla traiettoria, od un grave in caduta libera che parta da fermo, ove varia solo l'altezza. Un oggetto che si muova liberamente in un piano, come per esempio un proiettile che si muova inizialmente in due direzioni, ha invece due gradi di libertà, le variabili corrispondono alla coordinata x ed alla y.
Per ogni grado di libertà lo stato è dato dal valore della corrispondente variabile (posizione) e dalla velocità con cui quella variabile cambia (velocità).
Come si accennava in precedenza alcuni danno definizioni di stato piuttosto diverse, per esempio:
"The state of a system at a given instant is the set of numerical values which its variables have at that instant." (Ashby)
Se lo stato viene definito in questo modo esso è l'insieme dei valori di tutte le variabili "congelate" in un singolo istante. Con questa definizione sono variabili di stato tutte le variabili del sistema, ingressi ed uscite compresi. Per quanto questa definizione non piaccia all'Autore, si deve far rilevare che è quella accettata da molti altri. Chi definisce lo stato come "tutte le variabili di un sistema" di solito chiama "stato interno" le variabili di "memoria" del sistema, che noi abbiamo chiamato solo "stato".
Sistemi senza memoria o combinatori
I sistemi, statici o dinamici, che non hanno lo stato sono detti "combinatori". Dato che lo stato è la memoria di un sistema i sistemi combinatori sono senza memoria.
In un sistema combinatorio le uscite in un certo istante dipendono unicamente dai valori degli ingressi nello stesso istante.
Esempi:
Consideriamo il funzionamento di una calcolatrice tascabile. Se diamo in ingresso alla calcolatrice i tasti "1 + 1 =" il risultato sarà sempre 2, ciò indipendentemente da cosa è successo nel passato.
Dunque se si vede una calcolatrice "dall'esterno", senza considerare come funziona internamente, essa svolge una funzione di tipo combinatorio (almeno quando non si usa il tasto di memoria!).
Un altro esempio può essere quello della rete elettrica illustrata in Figura 5, parte a).
Il partitore resistivo risponde alla legge:
Vout (t) = R2 * Vin (t)
(R1 + R2)
Per cui se cambia il valore in ingresso, Vin (t), funzione del tempo, cambia istantaneamente anche quello dell'uscita, Vout (t), ed assume un valore che è indipendente da tutto ciò che è successo nel passato, ma dipende solo da Vin.
Dato che il ritardo nella risposta di un sistema è dovuto al fatto le variabili di stato accumulano gli ingressi al loro interno, si conclude che i sistemi combinatori non hanno ritardi.
E' abbastanza evidente che è impossibile trovare in natura sistemi combinatori "veri", dato che ogni trasformazione fisica richiede un tempo finito per essere eseguita.
Perciò a voler indagare con la massima introspezione il funzionamento di ogni sistema si potrà individuare, a qualche livello di dettaglio, un suo comportamento non combinatorio.
Ciò non impedisce di usare modelli combinatori per determinare il comportamento di moltissimi tipi di sistemi. Questi modelli sono del tutto adeguati in tutte le situazioni pratiche in cui i sistemi reali corrispondenti si vengono a trovare.
Sistemi con memoria o sequenzialiUn sistema dinamico che ha variabili di stato viene detto sequenziale.
 Dunque un sistema sequenziale contiene elementi di accumulazione, ha "memoria" di parte del passato e risponde con ritardo alle sollecitazioni che gli si impongono.
Dunque un sistema sequenziale contiene elementi di accumulazione, ha "memoria" di parte del passato e risponde con ritardo alle sollecitazioni che gli si impongono.
Figura 5: un sistema elettrico combinatorio (a) ed uno sequenziale (b)
Un esempio di circuito elettrico sequenziale è illustrato nella parte (b) della Figura 5.
Esso è un circuito "classico", usato per molte applicazioni e come modello per molti fenomeni fisici. Si tratta di un circuito RC, nel quale la grandezza di uscita Vout, il cui comportamento in risposta ad un ingresso a gradino è illustrato nella Figura 6 (la figura è ripresa dal programma "CircuitoRC.exe", incluso nel CDROM allegato).
Come si vede la risposta del sistema non è immediata. Si noti che sistema risponde con ritardo ma dopo un certo periodo di tempo produce un'uscita costante.
DA FARE
Figura 6: risposta di un circuito RC ad un gradino di tensione
Movimento di un sistemaSi definisce "movimento" di un sistema l'evoluzione del suo stato nel corso del tempo.
Condizione transitoria o condizione di regimePer principi fisici fondamentali ogni sistema fisico tende, se sottoposto ad ingressi regolari nel tempo, a raggiungere una condizione di equilibrio, statico o dinamico. La condizione in cui l'equilibrio è stato raggiunto viene detta condizione "di regime".
Un sistema si dice a regime quando, dopo un certo tempo da quando i suoi ingressi sono divenuti regolari, si è portato in condizioni statiche o stazionarie.
Un sistema "a regime" è quindi un sistema che si è portato in condizioni di equilibrio statico o dinamico, dopo un periodo in cui non era in equilibrio. Si è cioè "assestato" in conseguenza di una variazione ai suoi ingressi.
Nella condizione di regime lo stato del sistema si è stabilizzato, e di conseguenza lo sono anche le uscite.
Un sistema non a regime, nel quale le variabili non siano assestate, viene detto in condizioni transitorie.
Il periodo di tempo che va dalla variazione degli ingressi alla successiva condizione stazionaria viene detto transitorio. In pratica il transitorio è la condizione in cui è un sistema mentre si trova fra due condizioni di regime.
Esempio. Supponiamo di avere una molla con appesa una certa massa M, ferma. Il sistema è in condizioni di equilibrio statico. La forza peso della massa (Fp) viene equilibrata dalla forza applicata dalla molla (Fk), che perciò è un po' "tirata", come indicato nella Figura 7.
Supponiamo ora di dimezzare improvvisamente la massa appesa, nell'istante t1. Il sistema, inizialmente fermo, viene sottoposto ad un ingresso a gradino: la forza peso passa istantaneamente da M g a M g / 2.
La massa sale un po', poi comincia ad oscillare intorno al nuovo punto di equilibrio, oscilla durante il transitorio, poi a regime torna in un equilibrio statico, nel quale la molla è un po' meno "tirata" di prima.
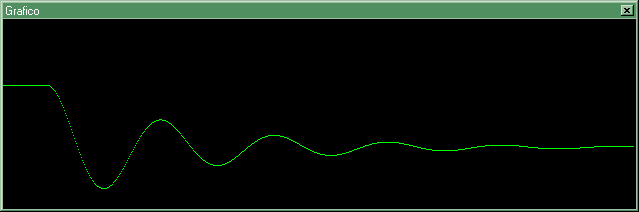 Figura 7: posizione di una molla eccitata con un ingresso a gradino (variazione della massa)
Figura 7: posizione di una molla eccitata con un ingresso a gradino (variazione della massa)
Nel CD ROM allegato a questo volume si potranno trovare alcuni programmi di simulazione che illustrano sistemi in cui sono presenti diversi tipi di equilibrio e che vanno a regime in tempi e modi diversi (c'è la simulazione di un pendolo, di una rete elettrica RC, ed altre). Con queste simulazioni si potrà sperimentare come i parametri dei sistemi influenzano il loro comportamento dinamico, la stabilità degli equilibri e quasi tutti gli altri concetti espressi in questo capitolo.
Nel caso del programma "Molla.exe" si può effettuare l'esperimento appena descritto e verificare il grafico del transitorio che si genera.
Il programma mette la molla inizialmente nel suo punto di equilibrio, che corrisponde ad un allungamento di 3,924. Da quel punto si può dare inizio al transitorio evidenziando il contenuto del text box "massa" e digitando 2. In questo modo la massa si dimezza improvvisamente ed il sistema comincia ad oscillare. Quando si sarà di nuovo fermato il valore di regime dell'allungamento sarà la metà del precedente.
Facciamo un altro esempio. Prendiamo una semplice rete elettrica RC, costituita da un resistore e da un condensatore, collegati come indicato in
Figura 8. L'ingresso è la tensione elettrica Vi, inizialmente nulla. Consideriamo inizialmente scarico il condensatore, ai cui capi è applicata una tensione nulla. Il sistema è quindi in equilibrio statico, non avendo "forze" applicate.
Ad un certo istante t0 la rete RC viene collegata alla rete elettrica nazionale. La tensione Vi diviene improvvisamente una tensione cosinusoidale del valore efficace di 220 V e della frequenza di 50 Hz (una tensione cosinusoidale ha la forma della funzione matematica "coseno" (cosinus)).
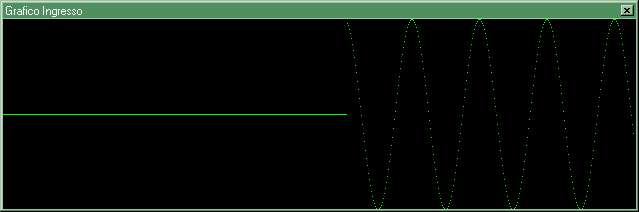 Inizia ora un periodo di transitorio, durante il quale l'uscita Vo "assomiglia" sempre più alla sinusoide che il sistema presenterà in uscita a regime. La sinusoide di uscita a regime è simile a quella di ingresso, anche se è sfasata ed ha valori di picco inferiori.
Inizia ora un periodo di transitorio, durante il quale l'uscita Vo "assomiglia" sempre più alla sinusoide che il sistema presenterà in uscita a regime. La sinusoide di uscita a regime è simile a quella di ingresso, anche se è sfasata ed ha valori di picco inferiori.
In condizioni di regime il sistema si trova in un situazione stazionaria, di equilibrio dinamico, nel quale il sistema "non cambia", anche se sia gli ingressi che lo stato e le uscite variano, in modo sinusoidale.
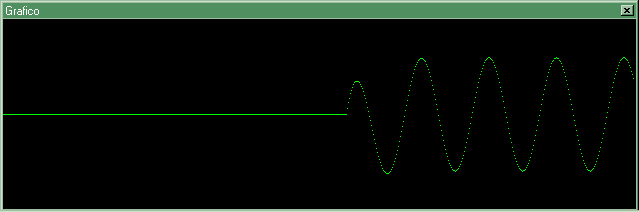
Figura 8: rete RC con ingresso sinusoidale, ingresso ed uscita (*)
(*)
Si può essere certi che, se gli ingressi sono sinusoidali, tali sono anche le uscite solo se il sistema è lineare, come accade in questo caso. Per la definizione di sistema lineare si veda il Capitolo 2Costante di tempo
Ogni sistema va a regime in tempi diversi, che dipendono dalle sue caratteristiche strutturali.
In alcuni sistemi semplici è possibile calcolare, con tecniche matematiche che non indagheremo, un numero che caratterizza la velocità con cui il sistema si assesta, cioè la durata dei transistori.
Questo numero è detto "costante di tempo", perché ha le dimensioni fisiche del tempo. Dopo un tempo corrispondente a tre o quattro volte la costante di tempo si può considerare esaurito il transitorio del sistema, in modo approssimativo ma valido per scopi pratici.
La costante di tempo di un sistema è dunque una misura della sua inerzia e non dipende dagli ingressi che gli si presentano (*), ma solo da come esso è fatto.
I sistemi complessi hanno molte costanti di tempo, anche molto diverse fra loro; la più grande è quella che più di tutte caratterizza i transitori, per cui spesso può essere presa, in modo approssimato, come unica costante di tempo di tutto il sistema.
(*) questo è senz'altro vero per i sistemi lineari, che saranno trattati in seguito, mentre può non essere vero per alcuni altri tipi di sistemi.
Nel programma di simulazione presente sul CD-ROM ("CircuitoRC.EXE") si potrà sperimentare l'effetto della variazione della costante di tempo del sistema.
Si può dimostrare matematicamente che la costante di tempo di un circuito elettrico RC è data dal valore R * C, cioè dalla resistenza del resistore moltiplicata per la capacità del condensatore.
Diminuendo i valori di R e/o di C si potrà osservare l'uscita rispondere più rapidamente alle variazioni degli ingressi.
Quando al sistema RC è applicato improvvisamente un ingresso, "accendendolo" con il check box "Abilita", l'uscita non varia istantaneamente, ma ha un ritardo di circa 3 volte la costante di tempo prima di andare a regime.
Alcune classificazioni dei sistemiDiamo ora alcune definizioni, che aggiunte a quelle già date, completano la nostra classificazione dei sistemi.
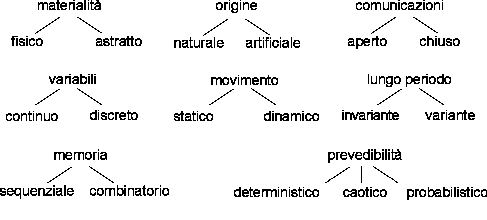 Tutte le classificazioni sono riassunte nella Figura 9. Nella figura le classificazioni sono associate ad una "parola chiave", relativa alla proprietà che distingue i vari tipi di sistemi classificati. La parola indicata in figura dovrebbe aiutare nella memorizzazione del relativo concetto.
Tutte le classificazioni sono riassunte nella Figura 9. Nella figura le classificazioni sono associate ad una "parola chiave", relativa alla proprietà che distingue i vari tipi di sistemi classificati. La parola indicata in figura dovrebbe aiutare nella memorizzazione del relativo concetto.
Figura 9: classificazioni dei sistemi
Sistemi continui o discretiUna variabile viene detta continua se, presi due suoi valori qualunque, essa può assumere anche tutti i valori intermedi.
Se invece vi sono alcuni valori "vietati", che essa non può mai assumere, la variabile viene detta discreta. La Figura 10 illustra graficamente quanto appena espresso a parole.
Una variabile continua per passare da un suo valore ad un altro deve assumere un numero infinito di valori, mentre una variabile discreta procede "a scatti" saltando da un valore all'altro ed assumendo un numero discreto di valori.
 Figura 10: variabili continue o discrete
Figura 10: variabili continue o discrete
Due definizioni più precise di variabile continua e discreta, che derivano direttamente dalla loro definizione matematica, sono le seguenti:
Una variabile è continua se i valori che può assumere possono essere messi in corrispondenza con l'insieme dei numeri reali o con un suo sottoinsieme.
.
Una variabile continua ha necessariamente un numero infinito di valori, dato che ogni sottoinsieme di numeri reali ha infiniti elementi.
Una variabile è discreta se i valori che può assumere possono essere messi in corrispondenza con l'insieme dei numeri naturali o con un suo sottoinsieme.
Dunque una variabile discreta può avere un numero infinito di valori, dato che i numeri naturali sono infiniti. Peraltro se una variabile può assumere solo un numero finito di valori essa è comunque discreta.
In sintesi, una variabile discreta ammette un numero di valori che "si può contare", almeno in linea di principio, se si ha la "pazienza" di farlo fino ad infinito .. .
Un sistema è continuo se tutte le sue variabili sono continue.
Se un sistema ha almeno una variabile discreta si dice "sistema discreto".
Un sistema potrebbe avere alcune variabili continue ed altre discrete. In un sistema discreto almeno una della variabili è di tipo discreto; quella variabile procede dunque "a scatti".
Un sistema potrebbe essere discreto in alcune variabili e continuo in altre; esempi di tali sistemi, che verranno trattari in dettaglio nei prossimi capitoli sono: il convertitore digitale – analogico (Capitolo 2), discreto negli ingressi e continuo nelle uscite, il convertitore analogico – digitale (Capitolo 2), continuo negli ingressi e discreto nelle uscite, gli automi a stati finiti (Capitolo 3), che hanno lo stato discreto.
Si può dire che un sistema è discreto nel tempo se la sua evoluzione procede "a scatti", il sistema mantiene il valore delle sue variabili per un intervallo di tempo, poi in un certo istante "scatta" e cambia istantaneamente il valore di tutte le sue variabili.
La gran parte dei sistemi fisici descritti dalla fisica classica è di tipo continuo, anche se molto spesso si usano modelli discreti per sistemi continui. Infatti molti sistemi discreti sono in qualche modo una semplificazione sono cioè modelli discreti di sistemi reali continui.
I sistemi continui sono spesso detti "analogici", per via del fatto che le loro variabili si possono misurare con strumenti che sono un modello analogico del segnale da misurare (vedi il paragrafo "Modelli fisici").
Sistemi invarianti o varianti
Un sistema invariante non cambia il suo comportamento nel tempo.
In un sistema invariante ingressi, stato e uscite possono essere variabili nel tempo, perché un sistema dinamico può senz'altro essere anche invariante.
Come già detto ciò che non cambia è il comportamento del sistema; questo ci porta ad enunciare una definizione più rigorosa di sistema invariante.
Un sistema è invariante nel tempo se, sottoposto in istanti diversi alla stessa sollecitazione, a partire dallo stesso stato, produce sempre lo stesso movimento e la stessa risposta.
Ciò significa che il sistema , sottoposto a due esperimenti identici in tempi diversi, si comporta sempre nello stesso modo.
Qualora i due esperimenti diano risultati diversi il sistema è cambiato nel corso del tempo, per cui si dice "variante nel tempo o "tempo – variante".
In parole povere si potrebbe dire che un sistema variante "invecchia" nel tempo.
Esempio:
Un dinamometro è uno strumento per la misura statica della forza, costituito da una molla, che viene sottoposta alla forza da misurare.
Se la forza è costante e il sistema è a regime la molla è deformata in modo diverso in base all'entità della forza applicata (Vedi ).
DA FARE
Figura 11: dinamometro
Per cui lo spostamento della molla misura la forza.
Se il dinamometro viene usato in modo improprio, per esempio se viene sottoposto ad un sovraccarico, la sua costante elastica può cambiare. Se misuriamo la forza peso di una massa campione in due momenti diversi, dato che la forza elastica è cambiata, cambierà la misura che otteniamo.
Questo significa che quel dinamometro è un sistema variante: ripetendo in tempi diversi lo stesso esperimento, con gli stessi ingressi e stesso stato "iniziale", si sono ottenute uscite diverse.
Il programma molla.exe del CD ROM allegato è la simulazione di un dinamometro. Si può sperimentare la deformazione a regime della molla effettuando i due esperimenti descritti, con costanti elastiche diverse (textbox "Rigidezza").
Prevedibilità di un sistema Sistemi deterministiciUn sistema deterministico è tale se possiamo conoscere univocamente, almeno in linea di principio, ogni elemento del suo stato in ogni istante.
Dunque se un sistema è deterministico ogni elemento del suo stato ha in un certo istante uno ed un solo valore (lo stato è "determinato").
Se ammettiamo di avere un buon modello di un sistema deterministico e di poter misurare il suo stato in un certo istante, sarà perciò possibile conoscere lo stato e le uscite del sistema in tutti gli istanti successivi, cioè prevederne "esattamente" il futuro.
Naturalmente la previsione esatta in senso matematico è impossibile per i sistemi fisici, per essi ci basta ottenere previsioni sufficientemente accurate ai fini pratici, per il problema che si deve affrontare.
Dunque ogni sistema fisico non è mai deterministico in senso stretto, ma la gran parte dei sistemi fisici non troppo complessi è approssimativamente deterministica per tutti i fini pratici.
D'altronde, se non fosse possibile prevedere e controllare il comportamento dei sistemi con sufficiente approssimazione, non esisterebbero persone disposte a farsi "sparare" su di un missile per raggiungere la luna!
Sistemi caoticiTutti i sistemi complessi esibiscono un comportamento molto difficile da prevedere; in molti sistemi è addirittura impossibile fare una previsione accurata e che duri per lungo tempo. Si pensi per esempio alla meteorologia o all'economia.
Ciò è dovuto alla molteplicità delle cause ed alla complessità delle relazioni fra gli elementi del sistema. Ma recentemente si è scoperto che questa non è la sola ragione dell'impossibilità di prevedere l'andamento di certi sistemi.
Infatti anche alcuni particolari sistemi molto semplici, dei quali il funzionamento è perfettamente noto e che ammettono anche modelli matematici deterministici hanno un comportamento che non è possibile prevedere in alcun modo.
Si pensi per esempio a quei soprammobili animati da un moto "perpetuo" perché contengono due magneti che si respingono, uno dei quali alimentato con un campo magnetico variabile. Essi continuano a muoversi sempre in modo diverso, le traiettorie non si "ripetono" quasi mai ed il moto è assolutamente "caotico". Per quanto il sistema sia semplice sarà impossibile prevedere cosa succederà fra qualche secondo, anche sapendo lo stato iniziale in modo molto preciso ed avendo un buon modello matematico del sistema.
Come esempio pratico prendiamo il modello di un pendolo fisico simulato nel programma PendoloCaotico.Exe, incluso nel CDROM allegato al libro.
Il pendolo fisico è un sistema che ha un modello matematico deterministico molto accurato. Dunque il pendolo si può "studiare bene" matematicamente ed il suo comportamento è facilmente prevedibile.
Supponiamo di applicare al pendolo una forza sinusoidale, che varia nel tempo sempre nello stesso modo. Il comportamento del pendolo è prevedibile entro certi campi della frequenza della sinusoide e della intensità della forza, in altri casi è del tutto "strano".
Trattazioni matematiche dettagliate (vedi http://www.gre.ac.uk/~fi437/) indicano che se la frequenza della forza è alta il pendolo ha un moto simile a quello di un pendolo normale, cui si aggiunge una componente casuale, che non influenza più di tanto il comportamento macroscopico del pendolo.
In altre condizioni invece il pendolo a regime produce un comportamento prevedibile, esibendo strane oscillazioni che però si ripetono indefinitamente.
Infine, se si aumenta la forza oltre una certa soglia, si vede che il moto del pendolo comincia ad assumere caratteristiche caotiche.
Il moto diviene del tutto irregolare ed imprevedibile.
Se si osserva come il pendolo si comporta si nota che per un certo tempo esso sembra ripetere certe oscillazioni, poi improvvisamente tutto cambia e le oscillazioni sono molto diverse.
Questo accade perché il sistema ha molti punti di equilibrio instabile, "vicini" fra loro, e si sposta continuamente fra moti intorno a quei punti, avvicinandosi ora all'uno, ora all'altro di quegli equilibri. Il sistema è molto sensibile a variazioni piccolissime delle condizioni iniziali, per cui basta molto poco per far spostare il suo movimento dai dintorni di un punto di equilibrio a quelli di un altro, cambiando in questo modo il suo comportamento in modo del tutto imprevedibile.
Rilevando periodicamente la posizione del pendolo è possibile determinare quanti sono i punti di equilibrio instabile attorno ai quali il pendolo caotico si muove, che possono essere trattati matematicamente usando gli strumenti della matematica frattale, una nuova branca della matematica che sta dando attualmente risultati molto interessanti.
Altri esempi di sistemi caotici, che promettono interessanti sviluppi applicativi: i neuroni del cervello durante le crisi epilettiche, le cellule del cuore durante un infarto.
Attualmente sono in corso studi per poter regolare i sistemi caotici, evitando che il loro comportamento diventi caotico oppure "imbrigliando" il caos per ottenere sistemi con migliori prestazioni.
Esempi di sistemi nei quali si potrebbero usare tecniche di regolazione caotica: pace maker di nuova concezione, aerei con ali a superficie variabile, più simili a quelle degli uccelli.
Molti sistemi deterministici, se sollecitati con ingressi troppo "forti" tendono ad entrare in una condizione caotica.
Un sistema caotico è senz'altro non lineare (vedi oltre per la definizione di linearità), in quanto i sistemi lineari non ammettono più di un punto di equilibrio: o sono "sempre" in equilibrio o non lo sono mai.
Sistemi stocastici
I sistemi stocastici, o probabilistici, sono quei sistemi dei quali, per ragioni pratiche o teoriche non è possibile dare una descrizione né deterministica né "caotica".
Le ragioni pratiche sono relative al costo: può non essere economico adottare strumenti deterministici, come nel caso della statistica demografica (studio delle popolazioni umane).
Per fare un esempio, ci si potrebbe chiedere: "quante persone in Italia stanno guardando la televisione in un certo istante?". Il problema è "facilmente" risolvibile in modo deterministico: basta telefonare contemporaneamente a tutti gli Italiani.
La cosa avrebbe un tale costo da non giustificare la risposta alla domanda, che peraltro è interessante.
Per dare comunque una buona risposta a quella domanda si deve studiare un numero ridotto di persone (un "campione" della popolazione) ed adottare tecniche matematiche che permettano di estendere i risultati a tutta la popolazione. Si utilizzano perciò strumenti di tipo probabilistico, cioè la teoria della probabilità e la statistica.
Possono esistere anche ragioni teoriche fondamentali che impediscono una analisi deterministica di certi sistemi.
Ciò accade per esempio nel caso dello studio dei sistemi subatomici (meccanica quantistica). Il quel caso il principio di indeterminazione ci impedisce di conoscere con esattezza la posizione di una particella in un dato istante, dato che il fatto stesso di rilevarne la posizione farebbe spostare l'oggetto dell'osservazione. Allora non si può affermare, in modo deterministico, che una particella è in un dato punto dello spazio in un certo istante, ma si può solo dare la "probabilità" che quella particella sia in quella posizione (questa è la funzione degli "orbitali" nella fisica delle particelle).
E' interessante far notare che le tecniche statistiche sono non deterministiche, quindi non danno risultati "perfetti", ma non sono "imprecise". Altrimenti non si spiegherebbe come i pubblicitari potrebbero decidere investimenti colossali in spot televisivi senza sapere "esattamente" quante e quali categorie di persone guardano la televisione ad una certa ora. Adottando tecniche statistiche non si è mai completamente "sicuri" dei risultati ma si possono avere risultati molto precisi. Anzi, si può dire che "pagando" si può avere la precisione che si vuole. Nel nostro esempio si può avere una maggiore precisione della statistica aumentando il numero e la varietà dei soggetti che vengono osservati mentre guardano la TV.
Una variabile di un sistema che deve essere descritta con metodi statistici viene detta "variabile aleatoria (*)" o "variabile stocastica".
Un sistema in cui almeno una variabile sia aleatoria viene detto "sistema stocastico" o probabilistico.
(*) il termine "aleatorio" proviene dalla parola latina "alea", che significa "dado". La ragione è intuibile ..
Alcuni esempi di classificazioni di sistemi
|
Sistema |
materialità |
origine |
Comunicazioni |
variabili |
movimento |
lungo periodo |
memoria |
prevedibilità |
|
Missile balistico |
Fisico |
Artificiale |
Aperto |
Continuo |
Dinamico |
Invariante |
||
|
Lavatrice |
Invariante |
|||||||
|
Gruppo di persone |
Fisico |
Naturale |
Aperto (di solito) |
Discreto (finito) |
Dinamico |
Variante |
Sequenziale |
|
|
Linguaggio parlato |
Astratto |
Artificiale |
Aperto |
Variante |
||||
|
Mucca |
Fisico |
Naturale |
||||||
|
Equazione algebrica |
Astratto |
? |
||||||
|
Edificio |
Fisico |
Artificiale |
Statico |
Invariante |
Combinatorio |
Deterministico |
Naturalmente alcune delle classificazioni precedenti sono questionabili e possono essere sottoposte a distinzioni e precisazioni più o meno sottili.
ModelliCome già accennato in precedenza un modello ed il sistema che esso deve descrivere possono essere molto diversi fra loro. Peraltro si può anche dare il caso che siano molto simili; tutto dipende dalle caratteristiche del sistema e del problema da risolvere.
In questo paragrafo classificheremo alcuni tipi di modelli e ne illustreremo le caratteristiche.
La prima distinzione da fare è fra due vaste categorie di modelli; una è quella dei modelli fisici (o reali) l'altra è quella dei modelli astratti (o simbolici).
Un modello reale è un sistema fisico ed è perciò costituito di elementi materiali, mentre un modello astratto è "intangibile".
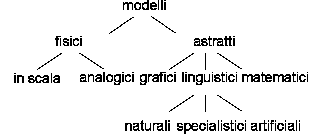 Nella Figura 12 si può osservare la gerarchia delle classificazioni che opereremo in questo paragrafo.
Nella Figura 12 si può osservare la gerarchia delle classificazioni che opereremo in questo paragrafo.
Figura 12: classificazioni dei modelli
Modelli fisiciIl prototipo è il tipo di modello più simile al sistema. Si tratta di un esemplare del sistema da studiare prodotto con le stesse tecniche e con gli stessi strumenti del sistema ed utile a verificare che tutto funzioni come dovuto prima di iniziare la produzione in grande scala del sistema, oppure a sperimentare verifiche da apportare ad esso.
Un prototipo identico può anche essere utile per verificare il comportamento del sistema originale quando esso non sia accessibile (questo accade per esempio con le copie delle sonde spaziali che vengono tenute a terra per risolvere i casi d'emergenza).
In generale i modelli fisici possono essere divisi in modelli in scala od analogici.
Un modello in scala è una versione, più piccola o più grande del sistema, che fa uso degli stessi principi fisici, cioè usa grandezze fisiche che hanno le stesse unità di misura, per realizzare un sistema che differisce all'originale solo nella scala.
Esempi di modello in scala sono i modellini che si usano per le prove in galleria del vento delle automobili da competizione. Spesso queste gallerie non possono essere molto grandi, dato che devono produrre un flusso d'aria ad una velocità piuttosto alta. Per questo i modellini sono più piccoli dell'auto da progettare, ma i risultati ottenuti su modello possono essere riversati sulla vera auto utilizzando i principi e le equazioni della fisica tecnica.
I modelli in scala possono anche essere delle stesse dimensioni dell'originale, come accade nelle grandi gallerie del vento, che accettano manichini in scala 1:1.
In un modello "analogico" vengono utilizzati principi fisici diversi da quelli del sistema originale.
Peraltro il comportamento del modello è "analogo" a quello del sistema (da qui il nome). Sperimentando su di esso si possono ricavare risultati utili nella risoluzione dei problemi del sistema originale.
Un modello analogico rimane un modello fisico del sistema, dato che la sperimentazione su di esso avviene applicandovi ingressi fisici e misurandone i risultati.
Esempio:
Fra circuiti elettrici ed idrodinamici esistono analogie di comportamento molto spiccate. Questo fatto è stato sfruttato nel passato per studiare con modelli elettrici il comportamento di condotte idrauliche.
La corrente che passa in un conduttore elettrico si comporta in modo analogo al flusso di acqua dentro la condotta forzata di una diga, le perdite di carico nella condotta sono analoghe alla resistenza di un resistore, il bacino di accumulo della diga si comporta come una capacità elettrica, la chiusa che regola il deflusso dell'acqua si comporta come un resistore variabile.
In un circuito idraulico all'apertura improvvisa di una chiusa (o di un rubinetto di casa!) si può innescare un fenomeno transitorio detto "colpo d'ariete" che crea una forte onda di pressione. Essa potrebbe anche distruggere la condotta.
Dato che è pericoloso provare il colpo d'ariete con le chiuse di una diga reale, un metodo impiegato nel passato era la costruzione di un modello equivalente alla diga (come indicato nella Figura 13(*)), la riproduzione delle condizioni dell'apertura della chiusa, e la registrazione della corrente che scorre nel circuito elettrico durante la fase transitoria.
La corrente registrata poteva poi essere associata per analogia alla portata d'acqua nella condotta forzata e di conseguenza alla pressione che la condotta avrebbe subito.
(*) Il modello illustrato in Figura 13, per quanto rappresenti la condotta ed il bacino, in realtà è una semplificazione troppo schematica del bacino idroelettrico, che in fase transitoria non potrebbe dar luogo a "colpo d'ariete".
 Figura 13: analogia fra circuito elettrico ed idraulico
Figura 13: analogia fra circuito elettrico ed idraulico
I modelli analogici sono stati molto usati quando non esistevano computer veloci come quelli odierni. Ai quei tempi era molto difficile ottenere indicazioni sui transitori dei sistemi, dato che era necessario risolvere complesse equazioni differenziali.
Al giorno d'oggi i modelli analogici sono stati sostituiti da modelli matematici simulati al computer.
Il termine "analogico" è usato in altri campi della tecnica. In alcuni casi viene usato con un significato non dissimile da quello illustrato in questo paragrafo. E' il caso per esempio della metrologia (scienza delle misurazioni); uno strumento di misura "analogico", fornisce sul suo quadrante una posizione dell'ago "analoga" alla grandezza misurata.
In altri casi si parla di sistema "analogico" in contrapposizione a sistema "digitale" (numerico). Questo significato è un po' improprio, per quanto molto usato. Infatti si dovrebbe piuttosto parlare di sistemi "continui" o "discreti", come abbiamo già visto.
Modelli astrattiI modelli astratti si possono classificare in molti modi. In questo paragrafo ne daremo una classificazione parziale ed illustreremo i principali tipi.
Tutti i modelli astratti fanno uso di simboli. E' una caratteristica primaria degli esseri umani fare uso di simboli, sia nelle comunicazioni fra di loro, sia nell'analisi e nel progetto dell'intervento umano sulla realtà.
Il modello che più spesso usiamo per rappresentare un sistema è la sua descrizione a parole nella nostra lingua.
Questo di spinge a classificare i modelli linguistici (o verbali), nei quali i simboli utilizzati, in forma scritta o parlata, sono le parole, articolate secondo le regole di un linguaggio.
Distinguiamo i linguaggi con cui si formulano questi modelli in tre categorie:
1) linguaggi naturali (o modelli linguistici naturali)
2) linguaggi specialistici o settoriali (o modelli linguistici specialistici)
3) linguaggi artificiali
Il linguaggio naturale è la lingua, scritta e parlata, di tutti i giorni. Esso nasce e si evolve nell'interazione fra gli esseri umani di una stessa comunità (nazionale o locale); è un'entità complessa ed in continua evoluzione che cambia con l'uso le sue regole e le sue consuetudini (in questo senso è un sistema dinamico e variante).
Proprio per la sua multiforme complessità il linguaggio naturale è soggetto a problemi di interpretazione e, spesso, di ambiguità nella formulazione dei concetti.
Vediamo un esempio. Nessun lettore avrà problemi a capire queste due frasi:
1 - Il marinaio salpò l'ancora, lenta la nave si staccò dalla banchina.
2 - "Mamma ancora, ancora!"
La parola ancora delle due frasi ha due significati estremamente diversi, che gli uomini capiscono al volo solo perché conoscono cos'è un marinaio, una nave, una banchina e sanno che i bambini di solito non posteggiano imbarcazioni.
In poche parole gli uomini capiscono il significato delle parole interpretando tutta la frase, cioè esaminandone il "contesto". La caratteristica fondamentale dei linguaggi naturali è che il significato delle sue frasi è fortemente dipendente dal contesto (*).
(*) si noti che un linguaggio naturale è un sistema artificiale, se teniamo valida la definizione di sistema artificiale come sistema realizzato intenzionalmente e per uno scopo specifico. Possiamo aggiungere anche questo agli esempi di ambiguità del linguaggio naturale!
Per rimuovere almeno in parte le ambiguità del linguaggio naturale le diverse comunità di esseri umani hanno modificato i linguaggi "generali" adattandoli alle caratteristiche dello specifico settore. Possiamo classificare fra i linguaggi settoriali il gergo degli informatici, quello degli avvocati o la lingua degli sportivi da bar.
Ma l'unico modo per rimuovere del tutto le ambiguità dei linguaggi naturali, che hanno troppe regole spesso in contraddizione, è inventare di sana pianta dei linguaggi artificiali.
E' indispensabile usare linguaggi artificiali quando la dipendenza dal contesto deve essere completamente eliminata.
Questo è il caso, per esempio, del linguaggio dei segni matematici, che è stato introdotto come modo non ambiguo ed universale di illustrare i risultati della matematica. Questo linguaggio non è solo indipendente contesto, ma anche dal linguaggio naturale di chi lo utilizza.
Un altro caso, molto importante per questo libro, di linguaggi artificiali, è quello dei linguaggi di programmazione per i computer.
Fino ad oggi i computer necessitano, per funzionare, di istruzioni non ambigue che specifichino completamente ciò che essi devono fare. E' chiaro quindi che il modo per presentare queste istruzioni ad un computer deve essere non dipendente dal contesto. Nel corso della storia dell'Informatica sono stati inventati centinaia di linguaggi di programmazione, solo pochi dei quali hanno avuto "fortuna" e consenso nella comunità dei programmatori.
Gli uomini usano molto spesso anche la grafica per modellare la realtà.
Confortati da detti popolari, quali "un disegno vale di più di cento parole", e dai risultati ottenuti, gli uomini si sono sempre espressi con disegni, quando hanno voluto ottenere messaggi di estrema stringatezza e di immediata comprensibilità.
I modelli grafici fanno uso molto spesso di simboli codificati.
Il consenso sul significato dei simboli può essere "locale" se è raggiunto all'interno di gruppi ristretti oppure "globale", se ottenuto attraverso veri e propri comitati di normalizzazione, come avviene, per esempio, con le norme UNI che stabiliscono i simboli da usarsi nel disegno tecnico.
Sono esempi di modelli grafici: cartelli stradali, disegno tecnico, disegno pubblicitario, ambiente operativo a finestre di un computer, diagramma di flusso di un programma, schema di un impianto elettrico.
Gli strumenti più potenti e flessibili che gli uomini hanno a disposizione per spiegare la realtà ed intervenire su di essa sono i modelli matematici.
Tutte le teorie scientifiche vengono in qualche modo rappresentate sotto forma di modello matematico.
Ogni teoria scientifica si confronta ogni giorno con la realtà e la sperimentazione, che richiedono che essa spieghi in modo soddisfacente le risultanze degli esperimenti e delle nuove scoperte. Se ciò non accede la teoria scientifica è da considerarsi falsificata.
Dunque se il modello matematico espresso dalla teoria non riproduce abbastanza fedelmente i risultati degli esperimenti è la teoria stessa che "cade".
I modelli matematici si esprimono molto spesso sotto forma di equazioni, risolvendo le quali è possibile prevedere il comportamento del sistema che essi rappresentano, o almeno sviluppare una sua analisi statistica.
Nel prossimo capitolo si andrà in maggiore dettaglio nella illustrazione dei modelli matematici.
Efficienza o efficacia di un sistemaPer concludere vogliamo puntualizzare la differenza fra due termini spesso usati come se fossero sinonimi, purtroppo anche dai tecnici, ma che hanno invece significati molto diversi.
I termini sono "efficacia" e "efficienza".
Un sistema è efficace quando fa "bene" il suo lavoro, cioè risponde effettivamente ai requisiti per i quali è stato ideato.
Un sistema è efficiente quando fa ciò per cui è stato ideato "spendendo poco".
Naturalmente serve una definizione più precisa per cui torniamo alla definizione fisica di rendimento:
![]()
h
(lettera greca eta) è il rendimento e rappresenta il rapporto fra l'energia trasformata, cioè quella parte dell'energia spesa che viene usata effettivamente per lo scopo che ci si prefigge e l'energia trasformabile, cioè tutta l'energia effettivamente spesa.Un sistema efficiente ha un alto rendimento.
Un sistema, ideale, che ha la massima efficienza ha rendimento 1 (100%). Non possono esistere sistemi reali con rendimento 1perché si violerebbero i principi della termodinamica. Nel sistema, ideale e quindi astratto, che avesse rendimento 1 tutta l'energia spesa sarebbe effettivamente utilizzata per lo scopo che ci si prefigge.
Quindi l'efficienza è una misura dell'energia sprecata. Tanto più è grande l'efficienza tanto più l'energia sarà meglio spesa per lo scopo voluto.
In pratica un sistema efficiente è quello che ottiene il massimo risultato con il minimo sforzo.
Molto spesso si sente usare la parola "efficienza" quando in verità andrebbe usata la parola "efficacia", che significa che un sistema svolge bene il suo compito.
Per esemplificare possiamo affermare che una Formula 1 ed un motorino sono entrambi sistemi ugualmente (poco) efficaci per andare a fare la spesa, dato che non hanno il bagagliaio. Il motorino sarà senz'altro più efficiente, sia come rapporto prezzi/prestazioni (nel traffico il motorino è veloce come la Formula 1!), sia per il consumo del carburante per ogni chilometro percorso.
I primi lavori "cibernetici" di Wiener, in tempo di guerra (1940), riguardarono lo sviluppo di un sistema automatico di "inseguimento" dell'obiettivo per le mitragliatrici antiaeree.
Esempio finaleConsiderando il sistema "lavatrice", identificare: un modello, gli ingressi del modello, le sue uscite, il suo stato, nei diversi casi in cui:
1) la si debba progettare
2) la si debba costruire
3) la si debba acquistare
4) la si debba utilizzare.
I modelli sono diversi in base all'uso che se ne deve fare
|
Uso |
Possibili modelli |
Ingressi |
Stato |
Uscite |
|
1) Progettare |
Schizzi di progetto |
Specifiche del management |
Raggiungimento di "pietre miliari" del progetto |
Il programma per il robot che la costruisce |
|
Modello per CAD |
Indicazioni dal mercato (marketing) |
I metodi di costruzione ed assemblaggio |
||
|
Schemi elettrici |
Vincoli sui materiali, i costi ed i modi di produzione |
Percentuale di avanzamento del progetto |
Il disegno esecutivo |
|
|
Il manuale d'istruzioni |
||||
|
2) Costruire |
Disegno esecutivo |
Materiali |
A che punto siamo nella sequenza delle istruzioni di assemblaggio? |
La lavatrice |
|
Programma per il robot |
Semiassemblati |
|||
|
Le spese per la produzione |
||||
|
Manodopera |
||||
|
3) Acquistare |
Depliant o disegno ornato |
Qualità / prezzo |
L'auto è pronta consegna? Se no, è già prodotta? Se sì, in quale deposito è? Se no quando verrà assemblata? Quando giungerà al concessionario? |
Acquisto / non acquisto |
|
Esemplare in esposizione |
||||
|
Aspetto |
||||
|
Dimensioni |
||||
|
Descrizione del venditore |
Garanzia |
|||
|
Condizioni d'acquisto |
||||
|
Finanziamenti |
||||
|
4) Usare |
Manuale d'istruzioni |
Tipo di biancheria da lavare |
Posizione del temporizzatore |
Panni lavati |
|
Bottoniera, temporizzatore |
Energia spesa |
Indicare alcuni problemi per i quali questo:
 può essere il modello di un uomo.
può essere il modello di un uomo.
Indicare alcuni problemi per i quali questi:
 possono essere il modello di "uomini". Discutere la differenza con il problema precedente.
possono essere il modello di "uomini". Discutere la differenza con il problema precedente.